The Medial Axis of a Multi-Layered Environment and its Application as a Navigation Mesh
Wouter van Toll, Atlas F. Cook IV, Marc J. van Kreveld, Roland Geraerts
ACM Transactions on Spatial Algorithms and Systems, vol. 4 (1), pp. 2:1-2:34, 2018.
Resources:
arXiv pre-print - ACM Digital Library page - Full paper (PDF)
Path planning for walking characters in complicated virtual environments is a fundamental task in simulations and games. A navigation mesh is a data structure that allows efficient path planning. The Explicit Corridor Map (ECM) is a navigation mesh based on the medial axis. It enables path planning for disk-shaped characters of any radius.
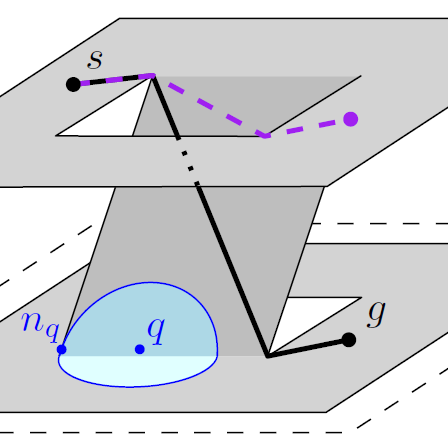
In this paper, we formally extend the medial axis (and therefore the ECM) to 3D environments in which characters are constrained to walkable surfaces. Typical examples of such environments are multi-storey buildings, train stations, and sports stadiums. We give improved definitions of a walkable environment (WE: a description of walkable surfaces in 3D) and a multi-layered environment (MLE: a subdivision of a WE into connected layers). We define the medial axis of such environments based on projected distances on the ground plane. For an MLE with n boundary vertices and k connections, we show that the medial axis has size O(n), and we present an improved algorithm that constructs the medial axis in O(n log n log k) time.
The medial axis can be annotated with nearest-obstacle information to obtain the ECM navigation mesh. Our implementations show that the ECM can be computed efficiently for large 2D and multi-layered environments, and that it can be used to compute paths within milliseconds. This enables simulations of large virtual crowds of heterogeneous characters in real-time.
@article{vanToll2018-MedialAxis,
author = {van Toll, W. and {Cook IV}, A.F. and van Kreveld, M.J. and Geraerts, R.},
title = {The Medial Axis of a Multi-Layered Environment and its Application as a Navigation Mesh},
journal = {ACM Transactions on Spatial Algorithms and Systems},
year = {2018},
volume = {4},
number = {1},
pages = {2:1--2:34}
}
